Help asap will give brainiest
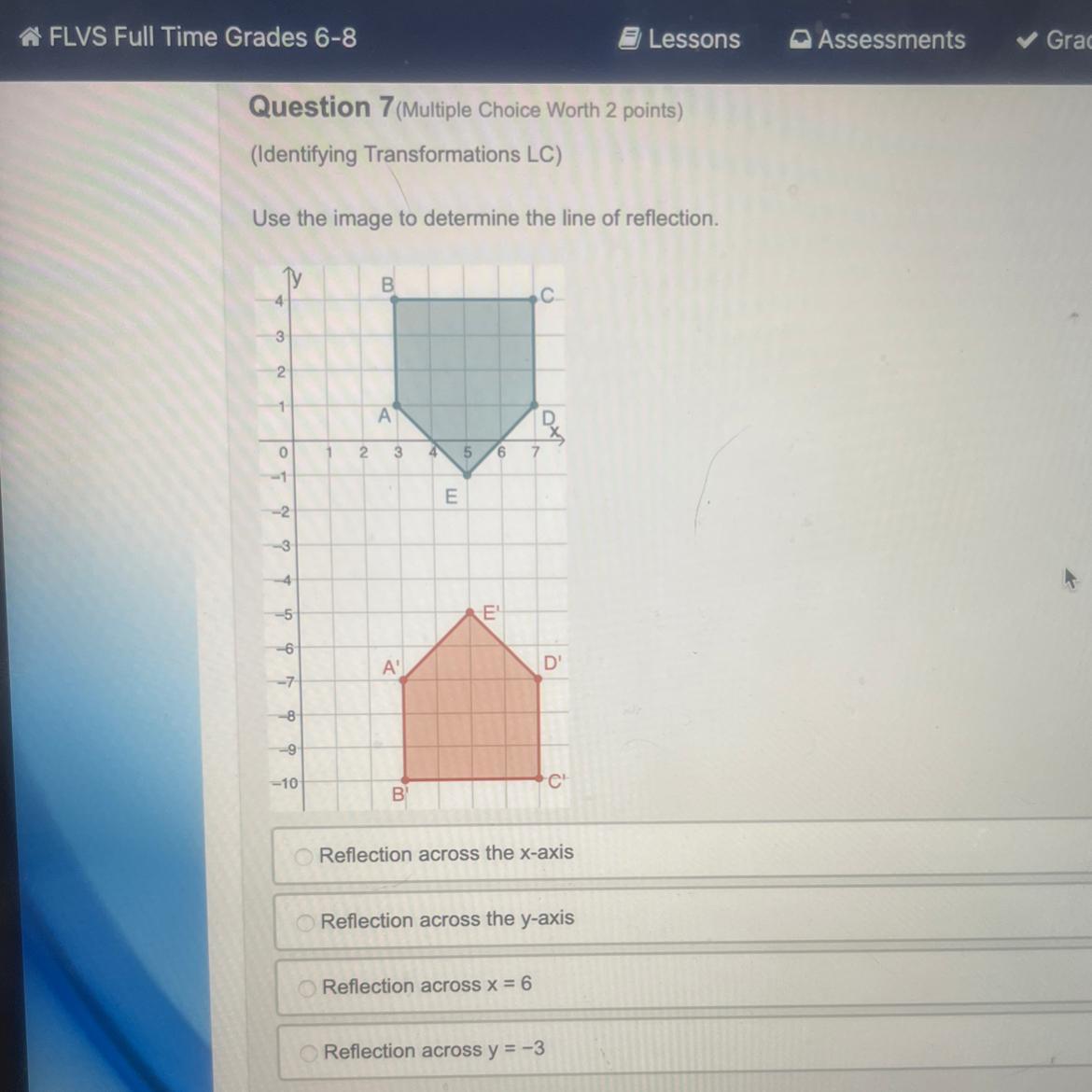
Use the image to determine the line of reflection.
4
3
2
1
0
?
Ty
5
-6
-7
-8
-9
-10
1
2
B
A
A
3₂
Α',
В'
4
E
5
E
6
с
Reflection across x = 6
D'
Reflection across the x-axis
Reflection across y = -3
C₁
Reflection across the y-axis
Answers
Answer: D
Step-by-step explanation: so if we look at the picture, youll notice 2 things right off the bat, firstly, the top shape goes over the y axis, so that wont work, secondly, the shapes are on the same side of the x axis (the positive side) so that wouldnt work, the last thing we now have to look at is making the shapes even, essentially if you were to flip one shape over a certain distance, the mirrored shape needs to be the same distance you flipped the first shape. In this case, if we flip shape 1, over -3, the other shape will be 6 spaces away from the 1st shape, because you need to also move the second shape 3 spaces away from where you flipped the first shape.
side note: reflecting over the x axis or y axis, means the line of reflection is equal to 0 on either the y axis or x axis
To try to make this less confusing, another way to find the reflection is by evenly counting the shapes to the middle, how-ever many squares/spaces it takes for both shapes to reach the center of the two in this case, is how many spaces they are reflected.
The image undergoes a reflection at y=-3, Option D is correct.
What is Graph?Graph is a mathematical representation of a network and it describes the relationship between lines and points.
A translation is a movement of the graph either horizontally parallel to the -axis or vertically parallel to the -axis.
Reflections are congruence transformations that generate a mirror image of an object, without changing its size or shape.
In the given figure the above image is original and it is flipped to form the image which is below the x axis.
In this case, if we flip shape 1, over -3, the other shape will be 6 spaces away from the 1st shape, because you need to also move the second shape 3 spaces away from where you flipped the first shape.
Hence, the image undergoes a reflection over y axis which is at y=-3.
To learn more on Graph click:
https://brainly.com/question/17267403
#SPJ5
Related Questions
20 points answer for brainlist
Multiply, Final answer needs to be in Standard Form.
−5m (−2m + m^2 − 4m^3 + 9)
Answers
Answer:
Using the distributive property, we can multiply -5m by each term inside the parentheses:
-5m(-2m + m^2 - 4m^3 + 9) = (-5m)(-2m) + (-5m)(m^2) + (-5m)(-4m^3) + (-5m)(9)
Simplifying each term:
= 10m^2 - 5m^3 + 20m^4 - 45m
The terms are arranged in descending powers of m, so this is already in standard form. Therefore, the final answer is:
20m^4 - 5m^3 + 10m^2 - 45m.
write 9 minutes and 25 seconds to 9 in the evening In analogue time
Answers
Answer:
9 minutes and 25 seconds to 9 in the evening in analogue time is represented as:
8:50:35 PM
1. Is the check register balance correct? If not, what is the correct balance?
Statement ending balance: $41.27
Outstanding deposits: $27.70, $12.30, $102.43
Outstanding check: $10.98
Service charge: $5.82
Check register balance: $78.50
2. The Smith's opened a savings account with a deposit of $500. If the interest rate is 4% per year compounded quarterly (every three months), what is the balance after 3 months? After 6 months? After 9 months? After 1 year
3. David put $1000 in a savings account that paid 8% interest compounded annually. How much interest was earned in year 1? What was the total balance at the end of year 1? What was the interest earned in year 2? What was the total balance at the end of year 2? Year 3?
4. Calculate the interest earned by the amount of these savings accounts and the total balance at the end of each year. The interest is compounded annually.
$100 at 7% for 4 years
$500 at 8% for 3 years
$300 at 6% for 5 years
5. Calculate the interest earned by the amount of these savings accounts and the total balance at the end of each year. Which is the better investment? Why? By how much?
$850 at 7% compounded annually for 3 years.
$850 at 7% compounded semi-annually for 3 years.
$850 at 7% compounded quarterly for 3 years.
Answers
1) the correct check register balance is $166.90.
2)
a) After 3 months, balance = $510.08
b) after 6 months, balance, = $520.40
c) After 9 months , balance = $531.07
d) After 1 year, balance = $542.50
3)
the interest earned in year 1 is $80,
the total balance at the end of year 1 is $1080,
the interest earned in year 2 is $86.40,
the total balance at the end of year 2 is $1166.40, and t
he interest earned in year 3 is $93.31, and
the total balance at the end of year 3 is $1259.71.
4)
the interest earned by the $100 savings account is $28, and the total balance at the end of 4 years is $128.
The interest earned by the $500 savings account is $120, and the total balance at the end of 3 years is $620.
The interest earned by the $300 savings account is $90, and the total balance at the end of 5 years is $390.
A check register balance is the amount of money in a bank account, as recorded by the account holder in their check register, after accounting for deposits, withdrawals, and fees.
1)
The check register balance is not correct. To find the correct balance, we need to adjust the statement ending balance for the outstanding deposits, subtract the outstanding check and service charge, and add any other transactions that may have been missed.
Adjusted balance for outstanding deposits: $41.27 + $27.70 + $12.30 + $102.43 = $183.70
Adjusted balance for outstanding deposits minus the outstanding check: $183.70 - $10.98 = $172.72
Adjusted balance for outstanding deposits minus the outstanding check minus the service charge: $172.72 - $5.82 = $166.90
Therefore, the correct check register balance is $166.90.
2)
To find the balance of the savings account after various time periods, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = the balance after time t
P = the principal (initial deposit)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = the time period (in years)
For this problem, we have:
P = $500
r = 0.04
n = 4 (compounded quarterly)
t = 0.25 (3 months), 0.5 (6 months), 0.75 (9 months), 1 (1 year)
After 3 months:
A = $500(1 + 0.04/4)^(4*0.25) = $510.08
After 6 months:
A = $500(1 + 0.04/4)^(4*0.5) = $520.40
After 9 months:
A = $500(1 + 0.04/4)^(4*0.75) = $531.07
After 1 year:
A = $500(1 + 0.04/4)^(4*1) = $542.50
Therefore, the balance of the savings account after 3 months is $510.08, after 6 months is $520.40, after 9 months is $531.07, and after 1 year is $542.50.
3)
To find the interest earned and total balance at the end of each year, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = the balance after time t
P = the principal (initial deposit)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = the time period (in years)
For this problem, we have:
P = $1000
r = 0.08
n = 1 (compounded annually)
t = 1 (year)
After year 1:
Interest earned = $1000 x 0.08 = $80
Total balance = $1000 + $80 = $1080
After year 2:
Interest earned = $1080 x 0.08 = $86.40
Total balance = $1080 + $86.40 = $1166.40
After year 3:
Interest earned = $1166.40 x 0.08 = $93.31
Total balance = $1166.40 + $93.31 = $1259.71
Therefore, the interest earned in year 1 is $80, the total balance at the end of year 1 is $1080, the interest earned in year 2 is $86.40, the total balance at the end of year 2 is $1166.40, and the interest earned in year 3 is $93.31, and the total balance at the end of year 3 is $1259.71.
4)
We can use the formula for compound interest to calculate the interest earned and total balance at the end of each year for each savings account:
$100 at 7% for 4 years:
P = $100, r = 0.07, n = 1 (compounded annually), t = 4
Interest earned = $100 x 0.07 x 4 = $28
Total balance = $100 + $28 = $128 after 4 years
$500 at 8% for 3 years:
P = $500, r = 0.08, n = 1 (compounded annually), t = 3
Interest earned = $500 x 0.08 x 3 = $120
Total balance = $500 + $120 = $620 after 3 years
$300 at 6% for 5 years:
P = $300, r = 0.06, n = 1 (compounded annually), t = 5
Interest earned = $300 x 0.06 x 5 = $90
Total balance = $300 + $90 = $390 after 5 years
Therefore, the interest earned by the $100 savings account is $28, and the total balance at the end of 4 years is $128.
The interest earned by the $500 savings account is $120, and the total balance at the end of 3 years is $620.
The interest earned by the $300 savings account is $90, and the total balance at the end of 5 years is $390.
Learn more about check register on:
https://brainly.com/question/11603816
#SPJ1
Simplify the expression to a polynomial in standard form
(x−3)(2x^2 −5x−5)
Answers
Answer:
Step-by-step explanation:
To simplify the expression, we can use the distributive property of multiplication:
(x−3)(2x^2 −5x−5) = 2x^3 −5x^2 −5x −6x^2 +15x +15
Next, we can combine like terms:
2x^3 −5x^2 −6x^2 −5x +15x +15 = 2x^3 −11x^2 +10x +15
Therefore, the simplified polynomial in standard form is 2x^3 −11x^2 +10x +15.
a package contains 6 blue, 4 red, and 5 yellow gumballs. You randomly choose a gumball from the bag, and you do not replace it. Then you randomly choose another gumball. What is the propobility of both gumballs not being red?
Answers
The probability of both gumballs not being red is 11/21.
What is the probability?
The probability of the first gumball not being red is:
P(first gumball not red) = P(blue) + P(yellow)
= (6/15) + (5/15)
= 11/15
After removing the first gumball, there are 14 gumballs left in the bag. The probability of the second gumball not being red depends on what color the first gumball was.
Case 1: The first gumball was blue
If the first gumball was blue, there are 5 blue, 4 red, and 5 yellow gumballs left in the bag. The probability of the second gumball not being red is:
P(second gumball not red | first gumball was blue) = P(blue or yellow)
= P(blue) + P(yellow)
= (5/14) + (5/14)
= 5/7
Case 2: The first gumball was yellow
If the first gumball was yellow, there are 6 blue, 4 red, and 4 yellow gumballs left in the bag. The probability of the second gumball not being red is:
P(second gumball not red | first gumball was yellow) = P(blue or yellow)
= P(blue) + P(yellow)
= (6/14) + (4/14)
= 5/7
The probability of both gumballs not being red is the product of the probabilities of each event:
P(both gumballs not red) = P(first gumball not red) * P(second gumball not red | first gumball not red)
P(both gumballs not red) = (11/15) * (5/7)
P(both gumballs not red) = 55/105
P(both gumballs not red) = 11/21
Therefore, the probability of both gumballs not being red is 11/21.
To know more about probability, visit:
https://brainly.com/question/11234923
#SPJ1
Number 5 Please look at image
Answers
The solutions to the quadratic equations are as follows
4a. The rocket was launched from an initial height of 10 meters.
b. The maximum height of the rocket was 55 meters.
c. The rocket reaches its maximum height at 3 seconds
d. the rocket is in the air for t = 6.316 seconds
5. when the horizontal distance is 1 foot, the height of the balloon is 8.875 feet
b. when the horizontal distance is 33 feet, the height of the balloon is 0.875 feet.
How do we solve the quadratic equation?The function is a quadratic equation, and here is how we solve each problem;
a. The initial height of the rocket is the value of h when t=0. So we substitute t=0 into the equation to find:
h = -5(0)² + 30(0) + 10 = 10 meters
b. & c. The maximum height of a projectile launched upward occurs at the vertex of the parabola represented by the quadratic function. For a quadratic function in the form y = ax² + bx + c, the time at which the maximum (or minimum) occurs is -b/2a. In this case, a = -5 and b = 30. So:
t = -b/2a = -30 / (2×-5) = 3 seconds
So, the rocket reaches its maximum height at t=3 seconds. We can find this maximum height by substituting t=3 into the equation:
h = -5(3)² + 30(3) + 10 = -5×9 + 90 + 10 = 45 meters
The rocket is in the air from the time it was launched until it hits the ground. The time when it hits the ground is when h = 0. So we can set the equation to 0 and solve for t:
0 = -5t² + 30t + 10
This is a quadratic equation and can be solved using the quadratic formula: t = [-b ± √(b² - 4ac)] / (2a)
Let's calculate the roots:
t = [-30 ± √((30)² - 4×-5×10)] / (2×-5)
= [-30 ± √(900 + 200)] / -10
= [-30 ± √(1100)] / -10
= 6.316 or -0.32
5. a. To find the height of the balloon when d=1, we substitute d=1 into the equation:
h = -1/8(1)²+ 4(1) + 5 = -1/8 + 4 + 5 = 8.875 feet
b. To determine whether the balloon hits your enemy, we need to see if the balloon's height (h) is above ground level (h > 0) when d=33. So, we substitute d=33 into the equation:
h = -1/8(33)² + 4(33) + 5
h = -1/8×1089 + 132 + 5
h = -136.125 + 132 + 5
h = 0.875 feet
when the horizontal distance is 33 feet, the height of the balloon is 0.875 feet. This means the balloon is above ground level and therefore would indeed hit your nemesis standing 33 feet away.
Find more exercises on quadratic equations;
https://brainly.com/question/26090334
#SPJ1
Write (Picture) as a fraction. Show your work.
Answers
23/200
Hope it helped
you can write 0.115 as a fraction in the
following way:
Let x = 0.115
Then 10x = 1.15
And 100x = 11.5
Subtracting the first equation from the second, we get:
100x - 10x = 11.5 - 1.15
90x = 10.35
Dividing both sides by 90, we get:
× = 10.35/90
Simplifying this fraction by dividing both the numerator and the denominator by 5, we get:
× = 2.07/18
Therefore, 0.115 is equal to the fraction 2.07/18.
I need help asap!!!!!
Answers
Answer:
8x - 58 ≤ 500
8x ≤ 500 + 58
8x ≤ 558
x ≤ 69.74
The ratio of James ' age to Andy's age is 2 : 7. In 8 years' time, the ratio will become
2 : 5, Find James' present age.
Answers
Answer: James' age now is 12 years old.
1.2541 rounded to nearest tenth
Answers
Answer:
1.3
Step-by-step explanation:
look at the hundredths place to decide how to round (1.2541).
when a digit is greater than or equal to 5, we round up
in this number, the hundredths place is 5, meaning we round up to get 1.3
i hope this helps :D
For problems 6 and 7 set up a proportion and solve.
pleaseeeee helpppp i’ll give brainlist
Answers
Using proportions we can find,
6. The weight of the adult bear = 750 pounds.
7. The measure of each angles are: 10°, 75° and 95°
Define proportions?In general, the term "proportion" refers to a part, share, or amount that is compared to a whole.
According to the definition of proportion, two ratios are in proportion when they are equal. Two ratios or fractions are equal when an equation or a declaration to that effect is utilized.
Here in the question,
The weight is in the ratio = 3:1000
The average birth weight = 12 ounces = 3/4 pounds.
Now the weigh of adult bear = 1000 × 3/4 = 750 pounds.
In the second part the angles are in the ratio, 2:15:19.
So, 2x+ 15x + 19x = 180
x = 180/36
x = 5
Hence, the measure of each angles are: 10°, 75° and 95°
To know more about proportions, visit:
https://brainly.com/question/30675547
#SPJ1
Mason’s pumpkin had a weight of 3 kg 250 g in August and 4 kg 125 g in October. What was the difference in weight from August to October?
Answers
Which relationships describe angles 1 and 2? Select each correct answer. O complementary angles O adjacent angles O vertical angles O supplementary angles
Answers
Answer:2
Step-by-step explanation:Because the 2 is closest to the middle line
Answer:
relationship describes angles 1 and 2 is supplementary angles. From the given figure
it is concluded that
the relation ship between angle 1 and 2 is supplementary angles
because its is linear pair
and forms a line
therefore , the angles are supplementary angles
hence , relationship describes angles 1 and 2 is supplementary angle
Step-by-step explanation: Hope this helps !! Mark me brainliest!! :))
HELPPPPP MEEEEEE!!! PLEASEEEEE
1.
Factor:
2x^2 + 9x + 18
What multiples to get 18 and adds to get 9?
a. (X+9) (x+2)
b. (X+6) (x+3)
c. (X-6) (x-3)
d. (X-9) (x-2)
2.
Factor:
X^2 - 20x + 36
What multiples to get 36 and adds to get -20?
a. (x-6) (x-6)
b. (x+3) (x+12)
c. (x-9) (x-4)
d. (x-18) (x-2)
3.
factor:
2x^2 - 5x -3
STEPS.
STEP 1* - Slide and Multiply the First Number to the Last
STEP 2 - Factor - What Multiplies to get the Last Number and Adds to get the
Middle Number?
STEP 3 - Divide and Reduce - The number we divide by is the same number we slid.
STEP 4 - Bottoms Up - If a fraction remains, move bottom number in front of the
variable.
*Unless there is a GCF. If there is, pull that out first.
a. (x-3)(x+1)
b. (2x+1)(x-3)
c. (2x-1)(x+3)
d. (x-3)(2x-3)
4.
what is the greatest common factor?
8x^2 + 18x + 4
a. 2
b. 4
c. 2x
d. 4x
5.
factor:
8x^2 + 18x + 4
STEPS.
STEP 1* - Slide and Multiply the First Number to the Last
STEP 2 - Factor - What Multiplies to get the Last Number and Adds to get the
Middle Number?
STEP 3 - Divide and Reduce - The number we divide by is the same number we slid.
STEP 4 - Bottoms Up - If a fraction remains, move bottom number in front of the
variable.
*Unless there is a GCF. If there is, pull that out first.
a. (x-2)(4x+1)
b. 2(x-2)(4x-1)
c. 2(x+2) (4x+1)
d. (x+2)(x+4)
Answers
The answer to the all questions was solved by the methods of factoring:
b. (x+6)(2x+3)c. (x-2)(x-18)a. (2x-3)(x+1)2b. 2(x-2)(4x+1)What is factoring?Factoring is the process of breaking down a mathematical expression or equation into simpler components, such as factors that when multiplied together give the original expression.
In the given questions,
1.Factoring 2x² + 9x + 18:
First, we need to find two numbers that multiply to 2×18=36 and add up to 9.The numbers are 6 and 6, since 6×6=36 and 6+6=12, but we need to adjust them to fit the middle term, which is positive.Therefore, we use 6 and 3: 6×3=18 and 6+3=9.We can write the expression as: 2x²+ 6x + 3x + 18.Now we can factor by grouping: (2x+6)(x+3).The answer is (a) (2x+6)(x+3).2.Factoring x² - 20x + 36:
First, we need to find two numbers that multiply to 36 and add up to -20.The numbers are -2 and -18, since -2×(-18)=36 and -2+(-18)=-20.We can write the expression as: x² - 2x - 18x + 36.Now we can factor by grouping: (x-2)(x-18).The answer is (d) (x-2)(x-18).3.Factoring 2x² - 5x - 3:
We can start by multiplying the first and last coefficients: 2×(-3)=-6.We need to find two numbers that multiply to -6 and add up to -5.The numbers are -6 and 1, since -6×1=-6 and -6+1=-5.We can write the expression as: 2x² - 6x + x - 3.Now we can factor by grouping: (2x-3)(x+1).The answer is (a) (2x-3)(x+1).4.Finding the greatest common factor of 8x² + 18x + 4:
We can start by factoring out any common factors of the coefficients, which is 2.Then we need to find the greatest common factor of the terms with x.The terms are 8x^2 and 18x, and the greatest common factor is 2x.The constant term, 4, is a factor of 2, so we can factor out another 2.The greatest common factor is 2(2x² + 9x + 2).The answer is (d) 4x.5.Factoring 8x² + 18x + 4:
First, we need to factor out any common factors, which is 2.Then, we can follow the steps:STEP 1* - Slide and Multiply the First Number to the Last: (2x+1)(4x+2).STEP 2 - Factor - What Multiplies to get the Last Number and Adds to get the Middle Number? The last number is 2, and the only factors are 1 and 2, which add up to 3, not 9. Therefore, the expression is prime and cannot be factored further.The answer is none of the given options.To know more about factoring expression, visit:
https://brainly.com/question/11994048
#SPJ1
Estimate!
16 3/4 divided by 2 1/2
Answers
Answer:7
Step-by-step explanation:
6.7 to the 10 is 7
this is a proportions question
Answers
In the above proportions problem, note that the distance of PR is 155.17ft.
What is the explanation for the above response?To solve for PR, note that
OC/RE = PR/OR
That is:
225/145 = PR/100
To solve for PR, we can cross-multiply the fractions:
225 * 100 = 145 * PR
22,500 = 145PR
Dividing both sides by 145:
PR = 155.17
Therefore, PR is approximately 155.17ft
Learn more about Proportions at:
https://brainly.com/question/31010676
#SPJ1
Explore Part 2
Using the numbers -4 to 4 without repeating, fill in the blanks to make a true statement.
One number will be unused. Use the sketch tool if it helps you with your thinking.
(N = unknown number)
N/N • N < N - N/N < N - N
Answers
4 number was not used in the statement. we can use -3 as the other value.
What is a statement?A simple statement is a single assertion that can be classified as true or false, while a compound statement is formed by combining two or more simple statements using logical operators such as "and", "or", and "not".
According to question:To explain the statement mathematically:
First, we evaluate N/N:
N/N = 1
Next, we simplify the inequality using this value:
1•N < N - 1 < N - N
Simplifying further, we get:
N < N - 1 < 0
We can then substitute the values of -4 to 4 for N and see which value(s) satisfy the inequality.
If N = -4, then we have:
-4 < -5 < 0
This is true, so we can use -4 as one of the values.
If N = -3, then we have:
-3 < -4 < 0
This is also true, so we can use -3 as the other value.
Therefore, the completed statement is:
-4/-4 • -4 < -4 - (-4/-4) < -4 + 4/-4 <br>
which simplifies to:
1 < -3 < 5/2
Note that one number, 4, was not used in the statement.
To know more about statement visit:
https://brainly.com/question/11823039
#SPJ1
Each cell in the crossnumber below contain a single non-zero digit. The answer
two-digit number.
What is the value of x?
A 1
21 UK Mathematics Trust
Clues
ACROSS
1. A square
3. An odd square
B 3
Down
1. A square
2. A square
C 5
www.ukmt.org.uk
1
3
D 7
2
X
Answers
The answer to the crossnumber is 25.
What is number?Number is a mathematical object used to count, measure, and label. It is a fundamental concept in mathematics and is used to describe sets, groups, and other mathematical objects. Numbers are used to measure quantities, such as length, area, time, and weight. They are also used to represent relationships between objects, and to describe the properties of those objects. Numbers can be represented in various forms, such as integers, fractions, and decimals.
This can be determined by examining the clues and their corresponding digits. Across, the clue is "A square", so the digit in the corresponding cell must be a perfect square, in this case 1. The next clue is "An odd square", so the digit must be an odd perfect square, which is 3. Down, the first clue is "A square", so the digit must be a perfect square, which is 5. The last clue is "A square", so the digit must be a perfect square, which is 7. When all the digits are put together, the resulting two-digit number is 25.
To know more about number click-
https://brainly.com/question/24644930
#SPJ1
100 Points!!! Algebra question, only looking for answer to last two. Graph each system of equations and describe it as consistent and independent, consistent and dependent, or inconsistent. Photo attached. Thank you!
Answers
1) y = -3x and y = -3x + 2: inconsistent system of equations.
2) y = x - 5 and -2x + 2y = - 10: consistent and independent.
3) 2x - 5y = 10 and 3x + y = 15 : consistent and independent.
Explain about the consistent and inconsistent system of equations?If there is at least one solution, an equation system is considered consistent. If there is no solution, a system is inconsistent.If one equation is a multiple of the other in a pair of equations that have two variables, both equations are dependant. Every point in dependent systems is a potential solution, giving them an endless number of solutions.The given equation are:
The graph for each system of equations is plotted.
1) y = -3x and y = -3x + 2
From the graph 1 it is shown that the lines for the each equation form the parallel lines.
Thus, system of equations are inconsistent.
2) y = x - 5 and -2x + 2y = - 10
From the graph 2 it is shown that the lines for the each equation form the coincident lines.
Thus, system of equations are consistent and independent.
3) 2x - 5y = 10 and 3x + y = 15
From the graph 2 it is shown that the lines for the each equation form the coincident lines.
Thus, system of equations are consistent and independent.
Know more about the inconsistent system of equations
https://brainly.com/question/19282045
#SPJ1
ASTORY OF RATIOS
Lesson 8 Problem Set 6.5
Plot the points for each shape, determine the area of the polygon, and then write an expression that could be used to
determine the area of the figure. Explain how each part of the expression corresponds to the situation..
1 A(1,3), B(2.8), C8, 8), D(10,3), and E(5,-2)
y
#D what is the area of this shape
Answers
Thus, the area of the pentagon formed by the given coordinates is:
A = 28.5 sq. units.
Explain about the pentagon?A pentagon is just a five-sided polygon in geometry having five straight sides and five inner angles totaling 540 degrees. A pentagon is a five-sided, flat (two-dimensional), plane geometric form.
The coordinates of polygon are:
A(1,3), B(2,8), C(8, 8), D(10,3), and E(5,-2).
Plot the points on the graph as shown.
The area of a pentagon calculation is used to determine the area of a pentagon with apothem, a, but one side length, s:
A = 1/2 * a * (5s)
a = apothem, of perpendicular distance from the centre.
s = length of side.
From graph:
s = 6 units.
a is calculated using the tan function.
each interior angle of pentagon = 54 degrees.
So,
tan (54/2) = a/ (s/2)
tan (36) = a/3
a = 3*tan (36)
a = 1.90 units
A = 1/2 * 1.90 * (5*6)
A = 28.5 sq. units.
Thus, the area of the pentagon formed by the given coordinates is:
A = 28.5 sq. units.
Know more about the pentagon
https://brainly.com/question/11759904
#SPJ1
Do you guys know the answer please help?
Answers
The value of x in the figure such that Ray YU is an angle bisector is 18 degrees
How to determine the value of x in the figureGiven
The figure
Such that Ray YU is an angle bisector
An angle bisector is a line or a ray that divides an angle into two equal parts or halves.
In other words, an angle bisector divides an angle into two smaller angles with equal measures.
The point where the angle bisector intersects the opposite side is the angle bisector point
This means that
2x = 36
So, we have
x = 18
Hence, the value of x in the figure is 18
Read more about angle bisector at
https://brainly.com/question/24334771
#SPJ1
The following ordered pairs are found on the graph of the same line.
(-3,9), (-1,4), (1, -1)
Which one of the following points would NOT be found on the line?
A.(-7,19)
B.(7,-16)
C.(-8,20.5)
D.(8,-18.5)
Answers
the point that would not be found on the line is option A, (-7,19).
How to calculate the line?
We can use the equation of the line that passes through these three points to determine which of the given points would not be on the line.
First, we can find the slope of the line using the first two points:
slope = (y₂ - y₁)/(x₂- x₁) = (4 - 9)/(-1 - (-3)) = 5/2
Now, we can use the point-slope form of the equation of a line with the slope we just found and the first point (-3,9):
y - y₁= m(x - x₁)
y - 9 = (5/2)(x + 3)
Simplifying this equation gives us:
y = (5/2)x + (27/2)
We can check that the third point (1,-1) also lies on this line by plugging in the values of x and y into the equation above.
Now, we can check which of the given points would not be on this line by plugging in the values of x and y into the equation above.
A. (-7,19): y = (5/2)(-7) + (27/2) = 5.5, which does not equal 19, so this point is not on the line.
B. (7,-16): y = (5/2)(7) + (27/2) = 22.5, which does not equal -16, so this point is not on the line.
C. (-8,20.5): y = (5/2)(-8) + (27/2) = 4.5, which does not equal 20.5, so this point is not on the line.
D. (8,-18.5): y = (5/2)(8) + (27/2) = 25.5, which does not equal -18.5, so this point is not on the line.
Therefore, the point that would not be found on the line is option A, (-7,19).
To know more about line visit :-
https://brainly.com/question/24644930
#SPJ1
A sphere has a surface area of 60 square feet. Which choice is the best approximation of its radius? Use 3.14 to approximate pi.\
Answers
Answer:
Step-by-step explanation:
The surface area of a sphere is given by the formula:
S = 4πr^2
where S is the surface area and r is the radius of the sphere.
We are given that the surface area of the sphere is 60 square feet. Using the formula above, we can solve for the radius:
60 = 4πr^2
Dividing both sides by 4π, we get:
15/π = r^2
Taking the square root of both sides, we get:
r = sqrt(15/π)
Using 3.14 as an approximation for π, we can evaluate this expression:
r ≈ sqrt(15/3.14)
r ≈ 2.20
Therefore, the best approximation for the radius of the sphere is 2.20 feet.
Answer:
Radius is 2.18
Step-by-step explanation:
;)
According to the 2016 issue of Sociological Statistics, in the 2015, the mean weight for boys
in the 4th grade is 64.9 pounds. If we assume the mean is still 64.9, find the probability that
the mean weight for 100 boys in the 5th grade will be between 60 and 70 pounds. Assume
that s = 17.5 pounds.
Answers
The probability that the mean weight for 100 boys in the 5th grade will be between 60 and 70 pounds is approximately 0.674.
What is central limit theorem?According to the central limit theorem, a statistical theory, regardless of the population distribution's form, the distribution of sample means tends to resemble a normal distribution as sample size grows. This implies that the distribution of the sample means will be about normal if we take several random samples from a population.
Given that, mean weight for 100 boys in the 5th grade will be between 60 and 70 pound.
The z-score is given as:
z = (x - μ) / (s / √(n))
Substituting the values:
z = (70 - 64.9) / (17.5 / √(100)) = 1.143 = 0.674
z = (60 - 64.9) / (17.5 / √(100)) = -1.143 =0.674
Hence, the probability that the mean weight for 100 boys in the 5th grade will be between 60 and 70 pounds is approximately 0.674.
Learn more about central limit theorem here:
https://brainly.com/question/17092136
#SPJ1
the population of a small town can be modeled with the function P(t)=18,751(1,09)^(t). Which statement about this situation is true?
A.The population will decrease by 9%.
B. The population will increase by 9%.
C. The population will increase by 1.09%.
D. The population will decrease by 1.09%.
PLEASE HELP ASAP!!
Thank You!
Answers
Statement B is true: The population will increase by 9%.
What are function's different types?Various Functions:
A single function (Injective function) Many – one function. From onto function (Surjective Function) Function is into. polynomial operation.
P(t)=18,751(1.09)t is the population function, where t is the time in years.
The function's growth factor or multiplier, which is bigger than 1, is represented by the expression (1.09t). In other words, the population is growing over time.
Finding the difference between the final and starting values, dividing by the initial value, and then multiplying by 100% will give us the percentage growth in the population.
Let's contrast the population at t=0 and t=1 to see how they differ:
P(0) = 18,751(1.09)^0 = 18,751
P(1) = 18,751(1.09)^1 = 20,436.59
In the last year, the population has grown from 18,751 to 20,436.59.
The population has grown by the following amount:
[(20,436.59 - 18,751)/18,751] × 100% ≈ 9.0%
Thus, the population will grow by 9%, as stated in statement B.
To know more about Function visit:
https://brainly.com/question/14996337
#SPJ1
Factor by substitution: (3y−2)2−(3y−2)−2.
Answers
The simplification of the polynomial using factor by substitution is: ((3y - 2)⁴ - 1)/(3y - 2)²
How to factor Polynomial by substitution?Factoring polynomials simply means separating a polynomial into its component polynomials.
Sometimes, in the event that polynomials are particularly complicated, it is usually easiest to substitute a simple term and factor down.
We have the equation:
(3y - 2)² - (3y - 2)⁻²
Let 3y - 2 be denoted by S and as such we have:
S² - S⁻²
= S² - 1/S²
Using the denominator as factor, we have:
= (S⁴ - 1)/S²
Plugging 3y - 2 for S gives us:
((3y - 2)⁴ - 1)/(3y - 2)²
Read more about Polynomial at: https://brainly.com/question/17517586
#SPJ1
The perimeter of the base of a square pyramid is 48 inches. The height of the pyramid is 8 inches. What is the surface area of the pyramid? Responses
Answers
Answer:
To find the surface area of a square pyramid, you need to find the area of the base and the area of the four triangular faces, and then add them together.
First, let's find the length of one side of the base of the pyramid:
Perimeter of the square base = 4 x side length
48 inches = 4 x side length
Side length = 12 inches
Now we can find the area of the base:
Area of the base = side length squared
Area of the base = 12 inches x 12 inches
Area of the base = 144 square inches
Next, we need to find the area of each triangular face. To do this, we need to find the length of the slant height of the pyramid. We can use the Pythagorean theorem to do this:
Slant height squared = height squared + (1/2 base length) squared
Slant height squared = 8 inches squared + (6 inches) squared
Slant height squared = 64 inches squared + 36 inches squared
Slant height = square root of (64 + 36) inches
Slant height = 10 inches
Now we can find the area of each triangular face:
Area of a triangular face = (1/2 base length) x slant height
Area of a triangular face = (1/2 x 12 inches) x 10 inches
Area of a triangular face = 60 square inches
Finally, we can add the area of the base and the area of the four triangular faces together to find the total surface area of the pyramid:
Total surface area = Area of the base + (4 x Area of a triangular face)
Total surface area = 144 square inches + (4 x 60 square inches)
Total surface area = 384 square inches
Therefore, the surface area of the pyramid is 384 square inches.
1. Convert from English to metric.
a 1 foot = _______ millimeters
b. 40 lb-ft = ________ Newton/meters
2. Convert from metric to English.
a. 30 lb = _______ kilograms
b. 90.8 qt = ______ liters
3. 26 m = _______ µm (micrometer)
4. 60,000 cm = _______ m
5. 8.275 L = _______ kL
6. 0.00349 km = _______ cm
7. 0.00175 mm = _______ nm
8. Name the metric system unit that measures each of the following:
a. Light intensity
b. Mass
c. Pressure
d. Electric current
e. Distance
9. 1,200 Ω = _______ kΩ (kilohm)
10. 120 kΩ = _______ Ω (ohm)
11. 3,500,000 Ω = _______ MΩ
12. 6.03 MΩ = _______ Ω
13. 0.000355 A = _______ µA (microampere) 14. 0.000355 A = _______ mA (milliampere)
15. 863 mV = _______ V (volt)
16. 657 Ω = _______ kΩ (kilohm)
17. 35 µA = _______ A (ampere)
18. 2.2 kΩ = _______ Ω
19. 500 kV = _______ MV (megavolt)
20. 7,500,000 µA= _______ A
21. What’s 30 percent of 150?
22. What’s 25 percent of 2,300?
23. Historically, the _______ was used as the basis for all measurements.
24. The number below the line in a fraction indicating the number of equal parts into which the unit is divided is the _______.
25. In the English system, _______ is the traditional unit of pressure.
26. The metric system is based on powers of _______.
27. What unit is used for time in the metric system?
28. 20°C equals _______°F.
29. 45°F equals _______°C.
30. The basic volume unit in the English measuring system is the _______.
31. One ounce equals approximately _______ grams
Answers
Answer:Convert from English to metric.
a. 1 foot = 304.8 millimeters
b. 40 lb-ft = 54.24 Newton/meters
Convert from metric to English.
a. 30 lb = 13.61 kilograms
b. 90.8 qt = 96.25 liters
26 m = 26,000,000 µm (micrometer)
60,000 cm = 600 m
8.275 L = 0.008275 kL
0.00349 km = 349 cm
Name the metric system unit that measures each of the following:
a. Light intensity - Candela
b. Mass - Gram
c. Pressure - Pascal
d. Electric current - Ampere
e. Distance - Meter
1,200 Ω = 1.2 kΩ (kilohm)
120 kΩ = 120,000 Ω (ohm)
3,500,000 Ω = 3.5 MΩ
6.03 MΩ = 6,030,000 Ω
0.000355 A = 355 µA (microampere)
0.000355 A = 0.355 mA (milliampere)
863 mV = 0.863 V (volt)
657 Ω = 0.657 kΩ (kilohm)
35 µA = 0.000035 A (ampere)
2.2 kΩ = 2200 Ω
500 kV = 500,000 MV (megavolt)
7,500,000 µA = 7.5 A (ampere)
What’s 30 percent of 150? = 45
What’s 25 percent of 2,300? = 575
Historically, the _______ was used as the basis for all measurements. = Human body
The number below the line in a fraction indicating the number of equal parts into which the unit is divided is the _______. = Denominator
In the English system, _______ is the traditional unit of pressure. = PSI (pounds per square inch)
The metric system is based on powers of _______. = 10
What unit is used for time in the metric system? = Second
20°C equals _______°F. = 68°F
45°F equals _______°C. = 7.2°C
The basic volume unit in the English measuring system is the _______. = Gallon
One ounce equals approximately _______ grams. = 28.35 grams
help True or false.
A poet can include figurative language and context clues to contribute to the overall meaning of a poem.
True
False
Answers
The correct answer is true
Answer:
True hope this helps!
si tengo 3657 manzanas y me quitan 84648 pero juan me regala otras 8469 cuantas me quedan para comer?
Answers
Answer:
0 (-72522)
Step-by-step explanation:
ahora tienes negativo manzanas